Power of compounding is essentially interest earned on interest re-invested or profits earned from profits re-invested. This concept is best understood through compound interest. In compound interest, the interest amount is added to the principal amount at the end of each period and interest is paid on the total amount.

 

For example, you invest Rs 100,000 for 3 years at an interest rate of 8% with annual compounding. At the end of the 1 year, you will earn interest of Rs 8,000 (8% of Rs 100,000). The earned interest is then added to the principal amount; therefore, the total amount of Rs 108,000 will now earn interest in the 2^nd year. At the rate of 8% per annum, in the 2nd year you will earn an interest of Rs 8,640. This accrued interest will be added to the principal amount of Rs 1 lakh and interest of Rs 8,000 earned in the 1^st year. The total invested amount is now Rs 116,640 (Rs 100,000 + Interest of 1^st years Rs 8,000 + Interest of 2^nd years Rs 8,640). Profits re-invested grow the investment value and you earn even more profits as the investment value increases over time. Over a long investment horizon you can create wealth through the power of compounding.

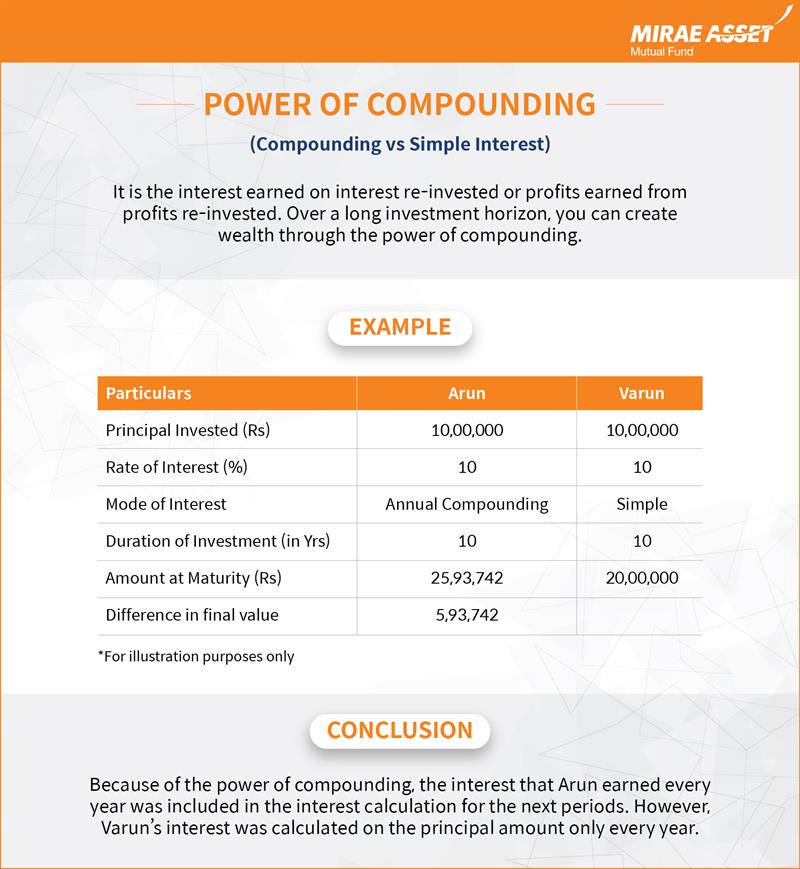
Let us understand it better through the table below* –

Particulars	Arun	Varun
Principal Invested (Rs)	10,00,000	10,00,000
Rate of Interest (%)	10	10
Mode of Interest	Annual Compounding	Simple
Duration of Investment (in Yrs)	10	10
Amount at Maturity (Rs)	25,93,742	20,00,000
Difference in final value	5,93,742

 

*For illustration purposes only

 

Arun and Varun both invested Rs 10,00,000 each in fixed deposits (FD) which pays 10% annual interest for 10 years period. Arun opted for a FD which offers compound interest (annually) whereas Varun opted for a FD which pays simple interest. As seen from the above table, at the end of the 10 year period Arun accumulates a corpus of Rs 593,742 higher than that of Varun’s corpus. Because of the power of compounding, the interest that Arun earned every year was included in interest calculation for the next periods. In case of Varun, however, interest was calculated on the principal amount only every year.  

We have seen the difference between compounding and simple interest.

 

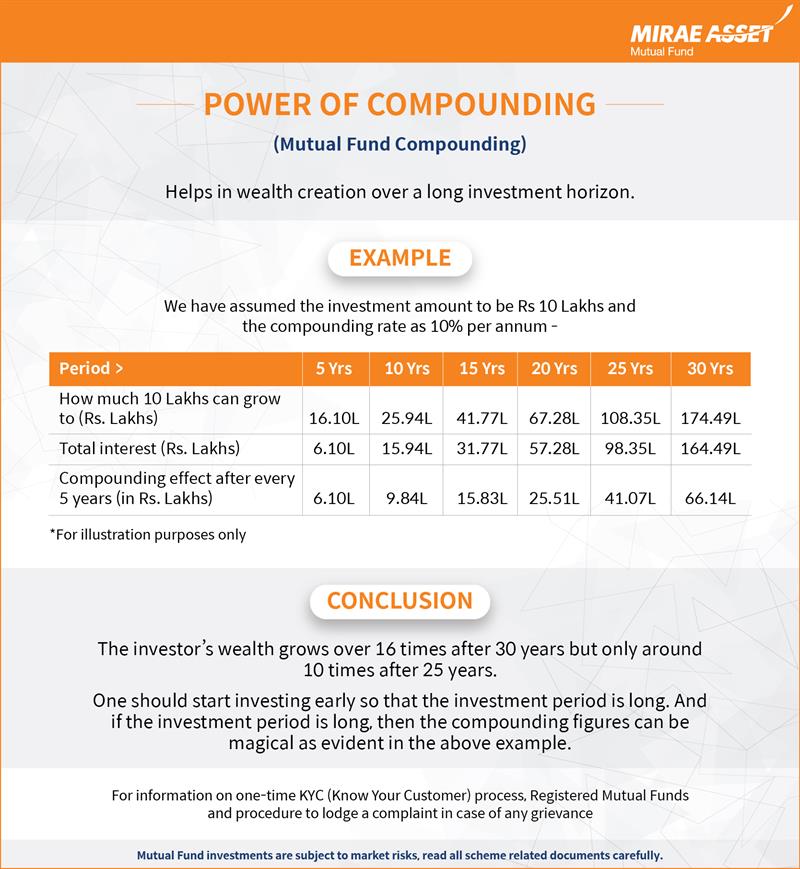
Now let us see, how compounding works in mutual funds? Mutual fund compounding can help in wealth creation in the long term as you can see through the table below – We have assumed the investment amount to be Rs 10 Lakhs and the compounding rate as 10% per annum -

Period >	5 Yrs	10 Yrs	15 Yrs	20 Yrs	25 Yrs	30 Yrs
How much 10 Lakhs can grow to (Rs. Lakhs)	16.10L	25.94L	41.77L	67.28L	108.35L	174.49L
Total interest (Rs. Lakhs)	6.10L	15.94L	31.77L	57.28L	98.35L	164.49L
Compounding effect after every 5 years (in Rs. Lakhs)	6.10L	9.84L	15.83L	25.51L	41.07L	66.14L

 

*For illustration purposes only

 

In the table above, we can see how Rs. 10 Lakhs invested over periods of 5, 10, 15, 20, 25 and 30 years grows to compounded values ranging from Rs 16.1 lakhs after the 5 year period to Rs 108.35 Lakhs after 25 years and Rs 174.49 Lakhs after the 30 years period.

Also visible is the additional amounts earned in each of the 5 years and how it is hugely growing from Rs 6.1 lakhs in the first 5 years to Rs 9.8 Lakhs in the next 5 years’ time and then to Rs 15.8 Lakhs, Rs 25.5 Lakhs, Rs 41.07 Lakhs and Rs 66.14 Lakhs respectively at the end of 15^th, 20^th, 25^th and 30^th year.

As you can see the investors wealth grows over 16 times after 30 years but only around 10 times after 25 years. The lesson here is that one should start investing early so that the investment period is long. And if the investment period is long then the compounding figures can be magical as evident in the above example.